지난 포스트에서 이어집니다.
이 포스트는 경희대학교 게임 그래픽 프로그래밍 수업자료를 바탕으로 합니다.
4. Geometry Shader
GPU에 의해 수행되는 셰이더 프로그램 중 하나로 HLSL, GLSL 등으로 작성된다. Primitives의 처리를 제어하며 vertex shader와 fragment shader단계 사이에 위치한다. 즉 점이나 선, 삼각형 등의 도형을 생성할 수 있는 기능이 있으며, 주로 테셀레이션이나 그림자 효과, 큐브 맵을 한번의 처리로 렌더링하는 데에 사용된다.
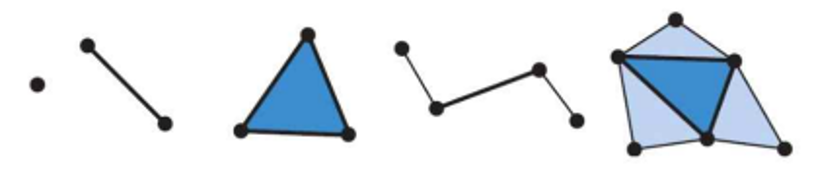
각 삼각형의 세 꼭짓점이 geometry shader에 입력되고 geometry shader가 Primitives 목록을 출력한다. vertex를 파괴하거나 만들 수 없는 vertex shader와 달리 geometry shader의 주요 장점은 geometry를 생성하거나 파괴할 수 있다는 것이다. 이를 통해 GPU에서 몇 가지 흥미로운 효과를 구현할 수 있는데, 예를 들어 입력 Primitive를 하나 이상의 다른 Primitives로 확장하거나, geometry shader가 어떤 조건에 기초하여 Primitive를 출력하지 않도록 선택할 수 있다.
5. Rasterizer
Rasterizer는 view에 없는 Primitives를 클립하고, Pixel shader 단계에 대한 Primitives를 준비하며, Pixel shader를 호출하는 방법을 결정한다. Rasterizer 단계에서는 실시간 3D 그래픽을 표시하기 위해 벡터 정보(shapes 또는 primitives로 구성됨)를 래스터 이미지(pixels로 구성)로 변환한다.
Rasterizer 단계에 도달하는 vertex는 몇 가지 고정된 vertex 후처리 단계를 거친다.
• Primitive Clipping
• Perspective Division
• Viewport Transform
즉, Resterization는 각 개별 primitive가 primitive의 샘플 적용 범위를 기반으로 Fragments(pixel shader)라고 하는 2차원 이미지 요소로 분할되는 프로세스인 것이다.
이 파트의 내용을 이해하기 위해서는, 먼저 클리핑에 대한 개념을 알아야 한다.
clipping은 clip space에서 이루어지지만 직관적인 이해를 위해 카메라 공간에서의 개념을 알아보겠다.
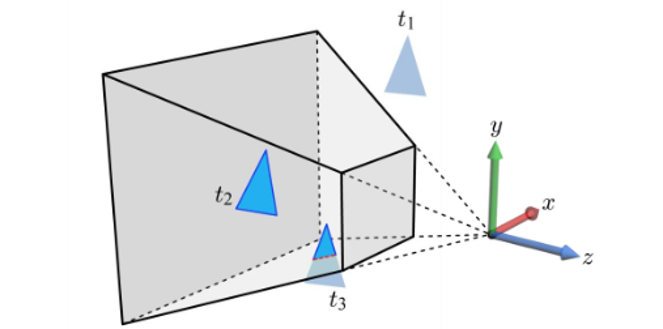
▪ 삼각형 t1은 view frustum에서 완전히 벗어나 컬링된다.
▪ 삼각형 t2가 완전히 안쪽에 있고 그대로 다음 단계로 넘어간다.
▪ 삼각형 t3은 view frustum와 교차하여 잘린다.
primitives가 클리핑 볼륨에 잘리는 방법은 기본 primitives 유형에 따라 다르다.
▪ Points : 포인트가 클리핑 볼륨 외부에 있으면 폐기된다. 점이 1픽셀보다 크면 점의 중심(SV_POSITION)을 확인한다.
▪ Lines : 선이 부분적으로 볼륨 외부에 있는 경우 새로운 vertex가 생성되어 클리핑 볼륨의 경계가 있는 끝점에 추가된다.
▪ Triangles : 삼각형이 viewing volume에 잘려지면 꼭짓점이 잘라내는 볼륨의 경계에 있는 적절한 삼각형이 생성된다.
5-1. Viewport Transform
큐브 형태의 공간에서 모니터 화면으로 넘어간다. 컴퓨터 화면의 창은 자체 창 공간 또는 화면 공간과 연결된다.
▪ viewport는 장면이 투영되는 화면 공간 직사각형을 정의한다.
▪ 전체 영역의 창일 필요는 없지만, 창의 하위 영역일 수 있다.
실제로 viewport는 다음과 같은 매개변수를 사용하여 3D 공간에서 정의된다.
▪ minX, minY, 너비, 높이, minZ, maxZ.
이를 설정하기 위해 D3D11_VIEWPORT 구조를 초기화한다.
▪vp.TopLeftX= minX, vp.TopLeftY= minY+ h, vp.Width= w, vp.Height= h
▪vp.MinDepth= minZ, vp.MaxDepth= maxZ
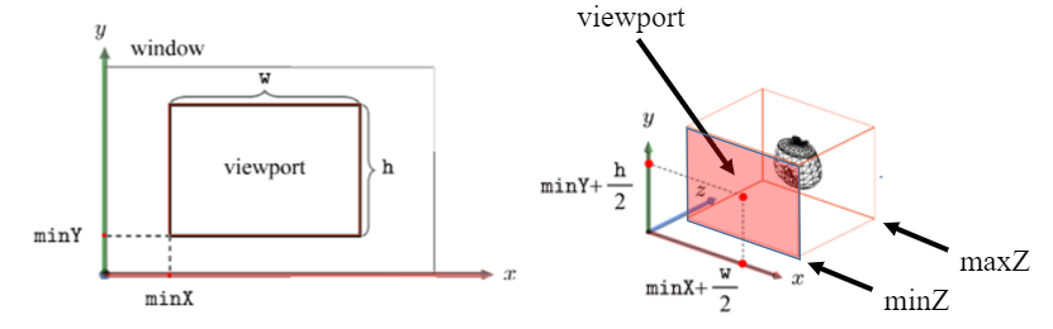
Viewport Transform은 vertex 위치를 NDC spacae에서 windoww space으로 변환합니다.
▪ scaling과 translation의 combination이다.
▪ DirectX에서 NDC 공간의 크기는 2×2×1인 반면 OpenGL에서는 2×2×2임을 기억하자.
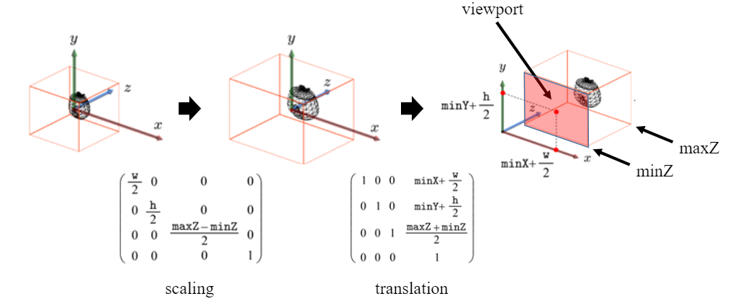
대부분의 응용 프로그램에서 뷰포트는 전체 창(모니터 화면)을 차지한다.
▪ minX = 0, minY = 0.
▪ minZ = 0, maxZ = 1.
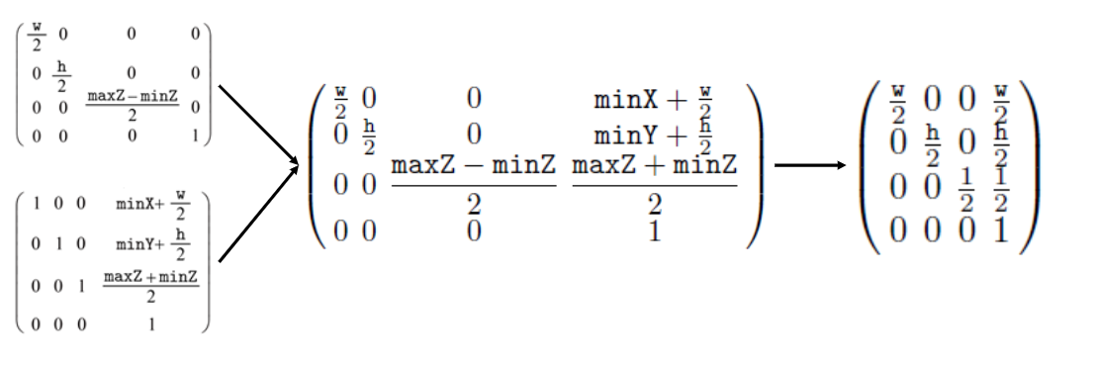
5-2. Face culling
Primitive에는 vertices의 순서로 정의되는 특정 면이 있다.
▪ 카메라 시점에서 멀어지는 Primitives를 back faces라고 한다.
▪ 카메라를 향하는 Primitives를 front faces라고 한다.
▪ Face culling을 사용하면 비싼 Rasterazation 및 Fragment shader 작업 전에 보이지 않는 기본 요소(back faces)를 제거할 수 있다. => 카메라에 보이지 않는 부분은 렌더링 하지 않는다.
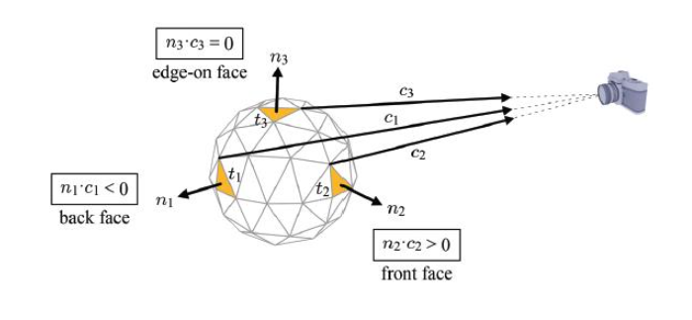
xy 평면에 보편적인 투영선을 따라 삼각형을 개념적으로 투영하자. CW 감기 순서의 2D 삼각형은 back face이고 CCW 감기 순서의 2D 삼각형은 front face이다.

아래 행렬식을 계산해보자. 여기서 첫 번째 행은 v1과 v2를 연결하는 2D 벡터를 나타내고, 두 번째 행은 v1과 v3을 연결하는 2D 벡터를 나타낸다.
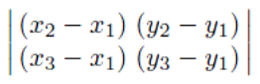
▪ If negative, CW and so back-face.
▪ If it is positive, CCW and so front-face.
▪ If 0, edge-on face.
back face가 항상 컬링되는 것은 아나다.
▪ 속이 빈 반투명 구를 렌더링하는 것을 생각해보자. bakc faces가 front faces을 통해 표시되도록 하려면 어떤 면도 컬링되어서는 안 됨을 알 수 있다.
DirectX의 Back face culling
▪ 기본적으로 face culling 활성화되어 있다.
5-3. Edge Equation
Primitives 래스터화는 두 부분으로 구성된다.
▪ 1. 윈도우 좌표에서 정수 그리드의 어느 사각형이 프리미티브에 의해 점유되는지 결정.
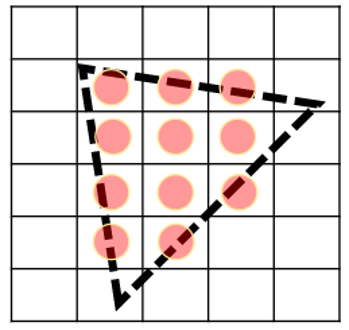
▪ 2. 그리드의 각 사각형에 색상 및 깊이 값 할당.
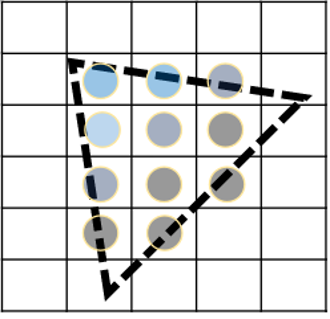
이를 바탕으로 다음 내용을 이해한다.
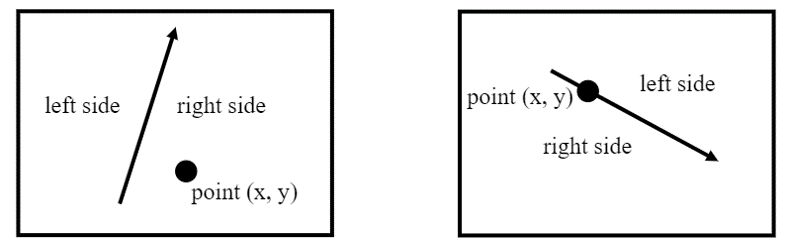
▪ 2D 평면을 두 부분으로 나누는 선이 있다고 가정하자.
- Edge Equation은 주어진 점이 이 선의 어느 쪽에 있는지 테스트한다.
• 점이 왼쪽에 있을 때: 음수.
• 점이 오른쪽에 있을 때: 양수.
• 점이 선 위에 있을 때: 숫자 0.
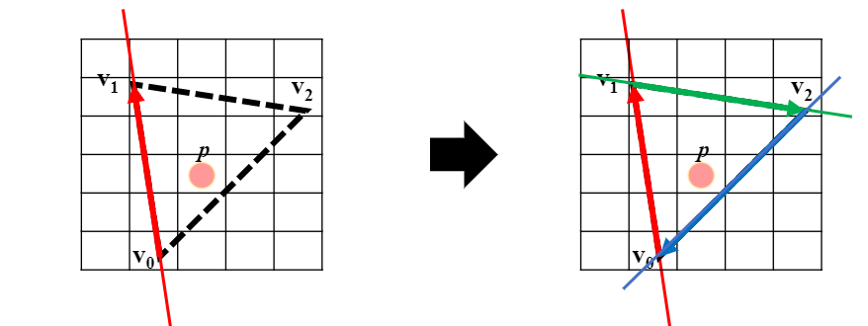
Edge Equation은 픽셀이 삼각형과 겹치는지 여부를 테스트한다.
▪ 삼각형의 모서리를 2차원 평면을 나누는 선으로 볼 수 있다.
▪ 삼각형의 첫 번째 변(꼭짓점 v0과 v1으로 정의됨)에 변 방정식을 적용해 보자.
▪ 이 예에서 픽셀은 선의 오른쪽에 있다.
▪ 다른 두 변에도 같은 방정식을 적용해 보자.
Edge Equation은 픽셀이 삼각형과 겹치는지 여부를 테스트한다. 아래 그림을 보자.
▪ 우리는 edge 함수가 삼각형의 세 모서리 모두에 대해 양수를 반환한다는 것을 확인할 수 있다.
▪ 점이 삼각형 안에 있는 경우 점은 삼각형의 세 모서리 모두의 오른쪽에 있다.
▪ 이는 edge 함수가 세 개의 edge 모두에 대해 양수를 반환함을 의미한다.
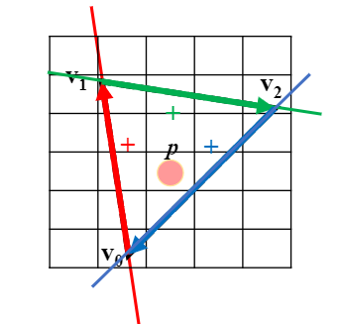
Edge Equation의 정의를 살펴보자.
▪ E(P, v0, v1) = (P.x–v0.x)·(v1.y –v0.y) -(P.y–v0.y)·(v1.x –v0.x)
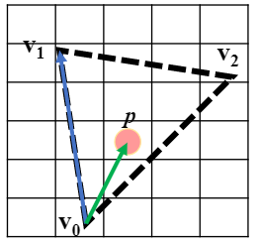
이 방정식은 2D 벡터(P-v0) 및 (v1-v0)의 구성요소에 의해 정의된 2×2 행렬의 행렬식 계산과 동일하다.
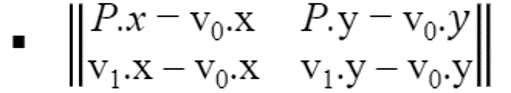
이 방정식은 수학에서 벡터 A = (P-v0), B = (v1-v0) 간의 외적 크기와 동일하다.
▪ 모든 3D 점(p, v0, v1)이 z값이 0이라고 가정해 보자.
▪ 그러면 다음과 같이 외적을 계산할 수 있다.
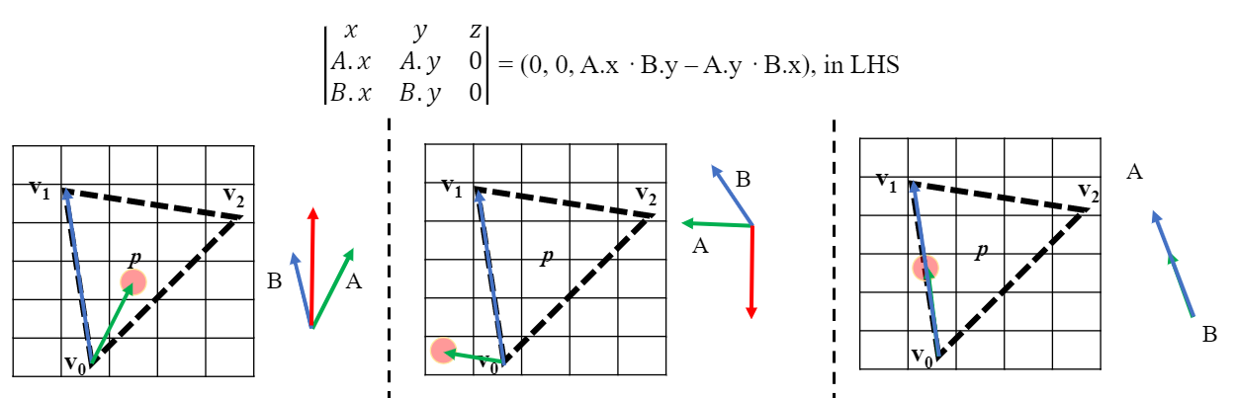
이 방정식은 수학에서 벡터 A = (P-v0), B = (v1-v0) 간의 외적 크기와 동일하다.
▪ (0, 0, A.x · B.y – A.y · B.x)에서 두 벡터의 외적 크기는 A.x · B.y – A.y · B.x임을 알 수 있다.
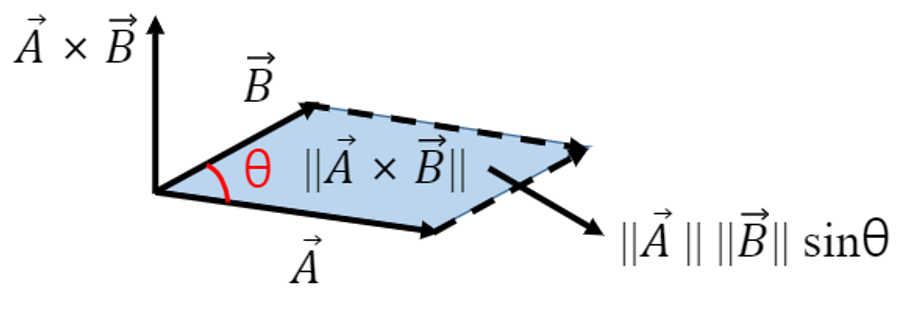
▪ 두 벡터의 외적의 크기는 오른쪽 그림과 같이 평행사변형의 넓이로 해석할 수 있으므로 위의 공식은 아래 그림의 결과와 같다는 것을 알 수 있다(평행사변형 공식).
▪ 따라서 edge 방정식은 0 < θ < 180이면 양수 값을 반환하고 180 < θ < 360이면 음수 값을 반환한다.
5-4. Assigning Attributes for Fragments
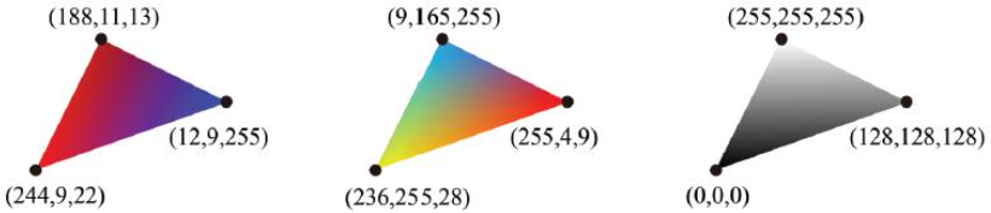
삼각형(v0v1v2)과 겹치는 점(p)의 속성(색상, 깊이, 법선 등)은 삼각형 꼭짓점의 속성을 보간하여 얻을 수 있다.
▪ v0, v1, v2의 색상이 Cv0, Cv1, Cv2라고 가정해보자.
▪ 그러면 p∈△V0,V1,V2에 대해 무게중심 좌표 P = λ0 * v0 + λ1 * v1 + λ2 * V2, λ0+λ1+λ2=1 로 p 의 색상을 계산할 수 있다.
▪ 위치, 깊이, 법선도 이 방법으로 계산할 수 있다.
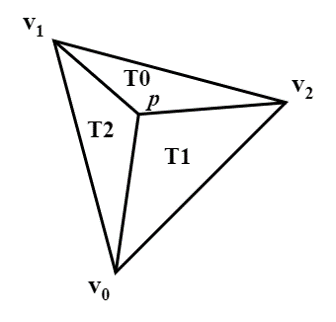
무게 중심 좌표(λ0, λ1, λ2)의 가중치는 삼각형(T0, T1, T2)의 면적에 비례한다. Edge Equation은 평행사변형의 면적을 반환하기 때문에, 아래와 같이 계산한다.
▪ T0은 0.5 * E(p, v1, v2)로 계산할 수 있다.
▪ T1은 0.5 * E(p, v2, v0)로 계산할 수 있다.
▪ T2는 0.5 * E(p, v0, v1)로 계산할 수 있다.
▪ 삼각형 v0v1v2의 넓이는 0.5 * E(v2, v0, v1)로 계산할 수 있습니다.
계산 공식은 아래와 같다.
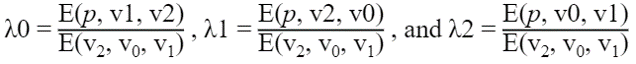
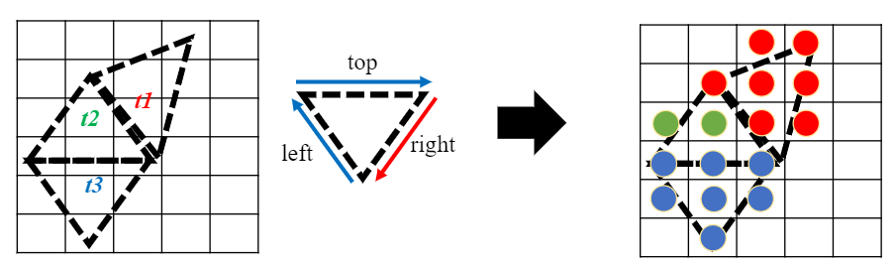
Top-Left 규칙 픽셀이 두 삼각형이 공유하는 edge에 있을 때 두 번 처리되는 것을 방지하기 위해 어느 삼각형에 속하는지 결정해야 한다. 이를 어떻게 처리하는지 알아보자.
▪ 그림을 보면 삼각형은 왼쪽, 오른쪽, 위쪽 또는 아래쪽 edge를 가질 수 있다.
▪ 아래 그림에서 t1은 왼쪽 edge 2개와 오른쪽 edge 1개, t2는 왼쪽 edge 1개, 오른쪽 edge 1개, 아래쪽 edge 1개, t3은 왼쪽 edge 1개, 오른쪽 edge 1개, 위쪽 edge 1개를 가진다.
▪ Direct3D는 픽셀이 삼각형의 위쪽 또는 왼쪽 edge에 있는 경우 그 삼각형에 속한다고 선언하는 top-left 규칙을 채택한다.
아래 그림을 보며 정확히 이해해보자.