이번 포스트부터 직접적으로 그래픽스를 알아보겠습니다. 이전 3개의 기본 개념 포스트는 이 번 포스트를 쉽게 이해하기 위한 빌드업 과정이었다고 생각해도 좋을 만큼 아마 오늘 내용이 가장 중요할 것입니다.
이 포스트는 경희대학교 게임 그래픽 프로그래밍 수업자료를 바탕으로 합니다.
1. GPU pipeline
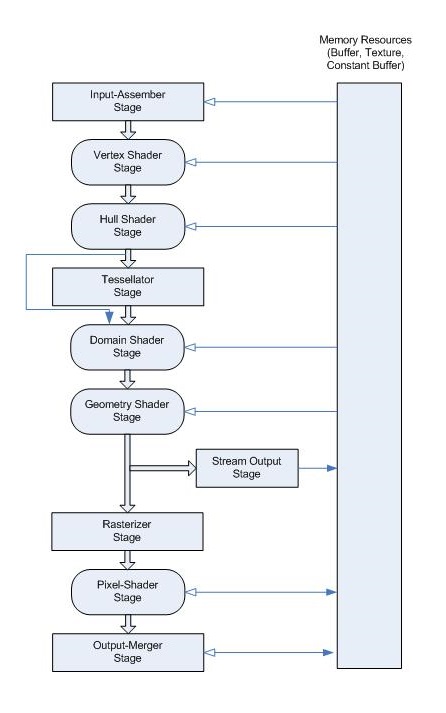
그래픽스 전체를 관통하는 핵심적인 구조이다. 위 사진의 구조는 반드시 알고 있어야 앞으로의 그래픽스 지식을 이해할 수 있다. 그래픽스 포스트에서는 이 중 3, 4, 5, 마지막 단계를 제외한 나머지 단계를 모두 알아볼 것이다.
GPU에서 렌더링은 한 단계의 출력이 다음 단계의 입력으로 사용되는 파이프라인 아키텍처에서 수행된다. 즉 위의 사진은 각 단계를 거치며 보여주는 입력에서 출력으로의 데이터 흐름이다.
▪ rendering pipeline의 shader는 program이라고 생각하면 이해하기 쉽다.
▪ 반면 Input-Assembly, Tessellation, Rasterization, Output-Merger Operation은 고정된 기능을 수행하는 hard-wired 단계이다.
2. Input-Assembly
파이프라인의 첫 단계. Input-Assembly는 primitives 또는 patches를 생성한다.
• 정점 정보(ex: position) 및 기하학적 기본 설정(ex: D3D11_PRIMITIVE_TOPOLOGY_TRIANGLELIST – gpu에서 받은 수많은 버텍스 정보를 3개씩 나누어 삼각형으로 인식하도록 함)을 사용한다.
• 입력이 6개의 꼭짓점의 시퀀스이고 기본 설정이 D3D11_PRIMITIVE_TOPOLOGY_TRIANGLELIST라고 가정하자. 그렇다면 출력은 두 개의 삼각형이 된다.
3. Vertex Shader
중요) per vertex -> clip space로 보낸다. 즉 스페이스 체인지가 일어난다.
vertex specifications은 Vertex shaders의 입력으로 사용된다.
▪ Vertex shaders는 정점마다 한 번씩 수행된다.
▪ Vertex shader는 각 정점의 최종 위치를 계산하기 위해 일련의 변환을 적용한다.

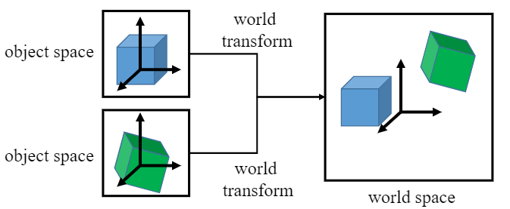
3-1. World Transform
world transform의 역할은 각각의 object space에 정의된 모든 objects를 world space이라는 단일 환경으로 조합하는 것이다.
3-2. View Transform
카메라를 기준으로 무언가를 찍는다고 생각하면 된다.
카메라도 객체이기 때문에 world space에서 정의된다. (3개의 기저를 필요로 한다 : xyz) world space의 카메라 포즈 사양은 다음과 같다.
▪ EYE: 카메라 위치
▪ AT: 카메라가 향하는 기준점
▪ UP: 카메라 상단이 가리키는 위치(view up vector), 대부분의 경우 UP은 월드 공간의 세로축인 y축으로 설정된다.
위 요소로 카메라 공간인 {u, v, n, EYE}를 생성할 수 있다. {u, v, n}은 직교기저(orthonorma basis)임을 기억하자.
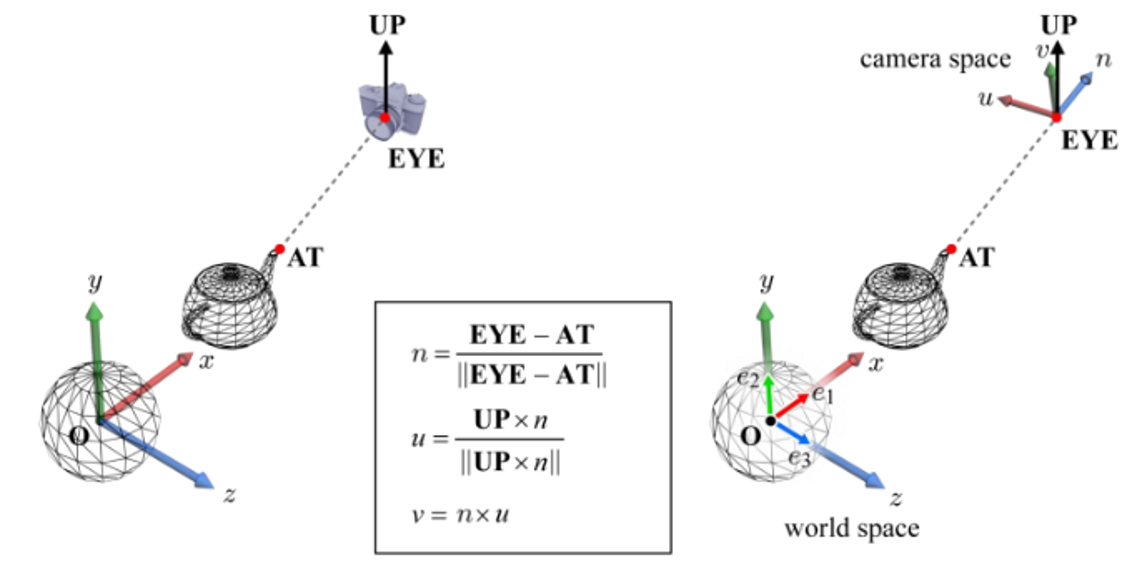
eye-at으로 n벡터를 구하고, n을 up벡터와 직교로 u를 구하고, n과 u로 v를 구한다.
예제와 함께 다시 살펴보자.
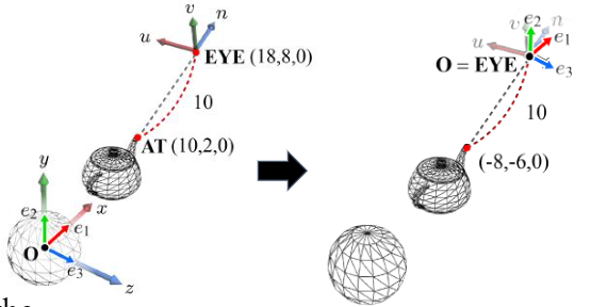
점에는 별개의 공간에서 서로 다른 좌표가 지정된다.
▪ camera space{u, v, n, EYE}와 world space{e1, e2, e3, O}.
▪ 찻주전자 입의 끝부분은 world space의 좌표(10, 2, 0)를 가진다.
▪ 찻주전자 입의 끝부분은 camera space에서 좌표(0, 0, -10)를 가진다.
▪ 모든 world space 객체를 찻주전자의 입 끝과 같이 camera space 측면에서 새로 정의할 수 있다면 렌더링 알고리즘 개발이 훨씬 쉬워질 것이다.
▪ 일반적으로 이를 space transform이라고 한다. world space{e1, e2, e3, O}에서 camera space{u, v, n, EYE}로의 공간 변경이 view transform인 것.
world space는 camera space {u, v, n, EYE}를 세계 공간 {e1, e2, e3, O}에 중첩하는 과정으로 직관적으로 설명할 수 있다.
▪ 첫째, EYE는 world space의 기원으로 translation된다.
▪ world space와 camera space는 이제 translation으로 인해 원점을 공유한다.
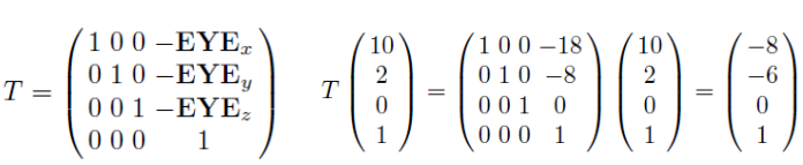
그런 다음 {u, v, n}을 {e1, e2, e3}으로 변환하는 회전 R이 필요하다. 그래픽스 기본 개념3에서 나온 rotation을 기억해보자.
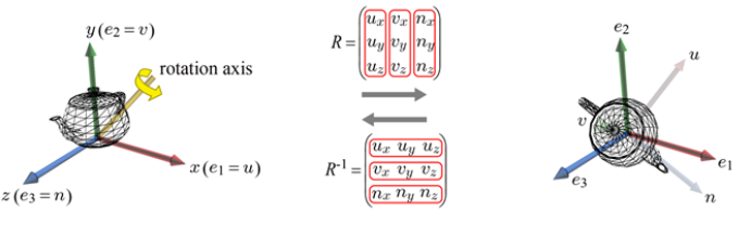
여기서 햇갈리기 전에, 위 개념에서 방향은 어떻게 정하는지 좀 더 확실히 정리하고 넘어가자.
Right-hand system Left-hand system을 떠올려 보자.
첫 번째 포스트에서 OpenGL은 RHS를 사용하고 Direct3D는 LHS를 사용한다는 것을 적어두었다. 이 차이를 알고 아래 내용을 보자.
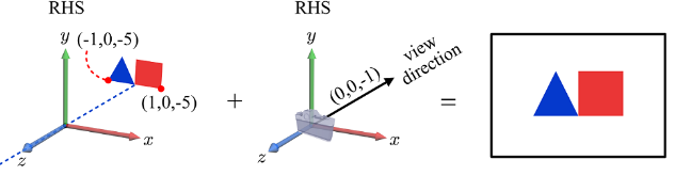
- RHS 예시
▪ 카메라의 위치(EYE) = (0, 0, 0)이고 카메라의 시야 방향(AT)이 (0, 0, -1)이라고 가정
▪ 카메라가 이미지를 캡처하면 아래와 같을 것이다.
- LHS 예시
▪ 객체 및 카메라 매개변수를 LHS로 이식해 보자. ▪ 꼭짓점의 좌표와 view의 방향은 바뀌지 않고 이미지가 뒤집힌 것을 알 수 있다.
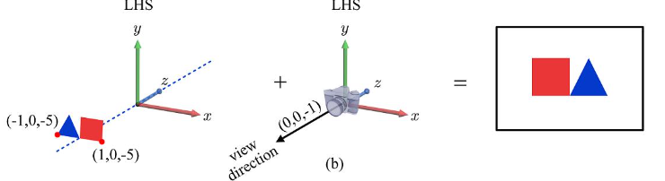
위 차이를 어떻게 보완해 줄 수 있을까?
▪ 위와 같이 반사적으로 나타나는 이미지 결과를 피하기 위해 객체와 뷰 매개변수의 z 좌표를 모두 무효화해야 한다. : z-negation
▪ z-negation은 개념적으로 z-축 반전과 동일하다.
즉, z축에 –1을 곱하는 것이다. (아래 그림에서 5에 –를 곱했다)

3-3. Project Transform
이전 과정에서의 eye, at, up은 카메라의 외부 파라미터이다. 카메라의 내부를 정의하는 것은 카메라 렌즈의 줌을 제어하는 기능 등을 말한다. 이를 살펴보자.
frustm과 culling에 대하여 알아보겠다.
View Frustum
▪ 카메라는 시야가 제한되어 있기 때문에, 장면의 모든 물체를 캡처할 수 없다.
▪ scene에서 보이는 영역을 view frustum(view volume)라고 한다.
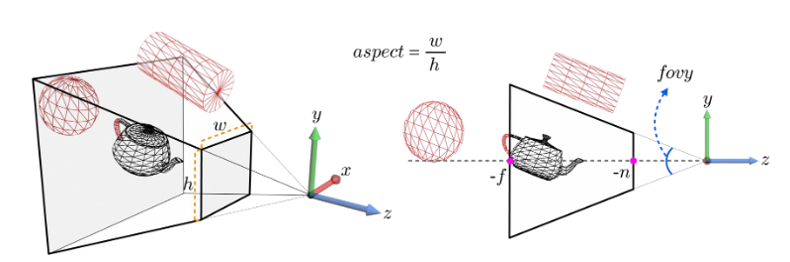
위 그림에서,
▪ view frustum parameters, fovy, aspect, n, f는 잘린 피라미드를 정의한다.
▪ fovy는 y축에 대한 시야를 지정한다.
▪ aspect는 뷰 프러스텀의 종횡비를 나타낸다.
View frustum culling
▪ out-of-frustum object는 최종 이미지에 기여하지 않으며 일반적으로 GPU 파이프라인에 들어가기 전에 폐기된다.
▪ 이 제거 과정은 GPU의 연산 능력을 절약한다.
Clipping
▪ polygon이 view frustum의 경계와 교차하면 경계를 기준으로 잘리고 view frustum 내부 부분만 처리되어 표시된다. (이는 래스터화 단계에서 수행된다)
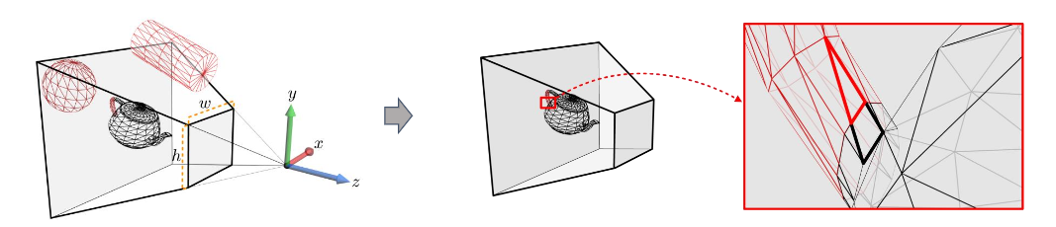
Clip space
▪ pyramidal view frustum은 클리핑에 사용되지 않는다.
▪ 대신, view frustum을 원점을 중심으로 축 정렬된 2×2×2 크기의 큐브로 변형하는 transform이 사용된다. 이를 projection transform이라고 한다.
▪ camera space objects는 projection transformed된 다음 큐브에 대해 잘리게 된다.
▪ projection-transformed 오브젝트는 clip space에 있다고 하며, 이는 이름이 변경된 카메라 공간일 뿐이다.
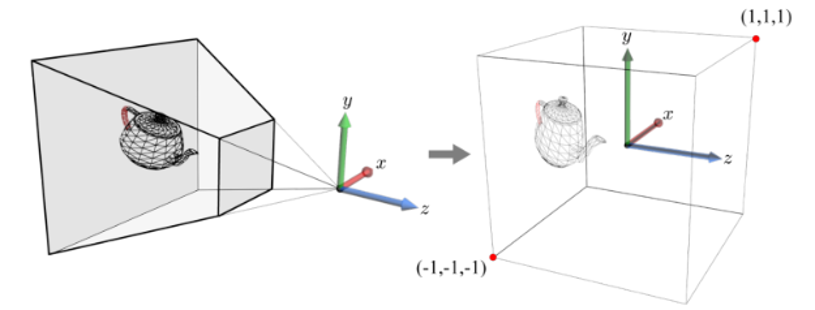
View frustum to cube
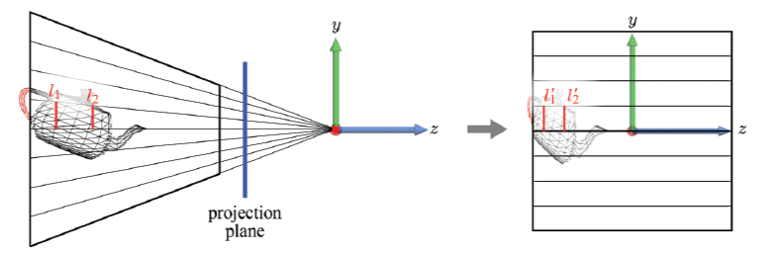
▪ view frustum은 마치 projection line의 연필(의 수렴하는 부분)로 볼 수 있다. 카메라(EYE)가 위치한 원점에 선이 수렴된다.
▪ 투영선의 모든 3D 포인트는 투영된 이미지의 단일 2D 포인트에 매핑된다. 멀리 있는 물체가 작게 보이는 원근 투영(perspective projection) 효과를 가져온다.
▪ projection transform은 projection line이 z축과 평행이 되도록 한다. 따라서 viewing은 보편적인 투영선을 따라 수행된다. projection transform은 “3D 공간 내에서” 원근 투영 효과를 가져온다.