저번 포스트 내용에서 이어집니다. 기본 개념은 이번을 마지막으로 하며, 다음 포스트 부터는 본격적으로 그래픽스 내용을 담게 됩니다.
이 포스트는 경희대학교 게임 그래픽 프로그래밍 수업자료를 바탕으로 합니다.
1. Affine transform
Affine에 대해서는, 수학적 계산 보다 기본적인 개념과 역할만 간단하게 알아본다.
두 Affine space U, V 간 Collinear point을 유지하는 Isomorphism으로 정의된다.
한 벡터공간을 다른 벡터공간으로 대응시키는 변환으로, 선형 변환과 평행 이동 변환의 합성으로 이루어져 있다.
▪ 3차원 공간은 Affine space이다.
▪ Affine transform이란, 점들을 변환하는 것이다.
▪ Affine transform은 직선을 보존하는 특징을 가지고 있다. 하지만 각도, 직선의 방향, 두 점 사이의 거리는 보존하지 않는다.
▪ 면적을 보존하지는 않지만, 면적이 변하는 배수는 일정하다.
▪ 주로 기하학적 왜곡이나 형태 변형을 보정하는데 사용된다.
ex) 위성 영상에서의 광각 렌즈 왜곡, 파노라마 스티칭, 영상 정합 보정
▪ 얼마나 많은 affine 행렬이 주어졌던지 간에 모두 행렬로 결합될 수 있다.
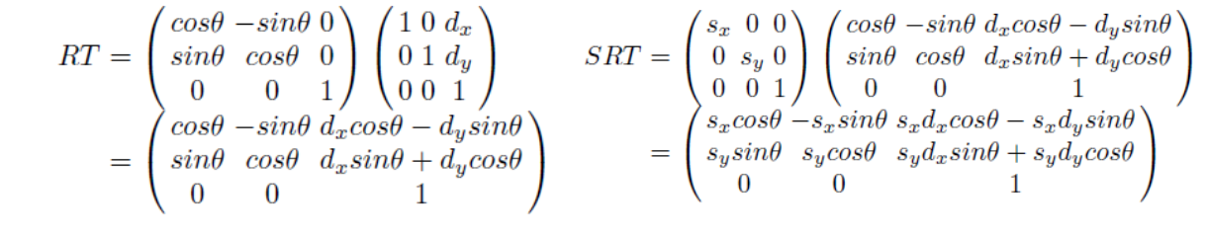
이와 반대로, Non-Affine transform은 다음과 같을 때 사용된다.
▪ 변환 후 공간의 평행선이 보존되지 않는 경우(ex.원근 투영)
▪ 선 사이의 중간 점이 보존되지 않는 경우(축을 따라 비선형 크기 조정)
2. Rigid motion (scaling을 제외한, rotation과 translation이 적용되는 모션)
▪ 결합된 affine 행렬을 객체에 적용하면 객체의 포즈(위치 + 방향)가 변경되지만 모양은 변경되지 않는다.
▪ 이런 의미에서의 변환을 rigid-bodymotion 또는 단순히 rigid motion이라고 명명한다.
▪ 얼마나 많은 회전과 평행 이동이 결합되었는지에 상관없이 결과 행렬은 [R|t] 구조이다.
▪ R은 translation을 포함하지 않는 combined rotation을 나타낸다.
▪ t는 rotation을 포함하는 combined translation 을 나타낸다.
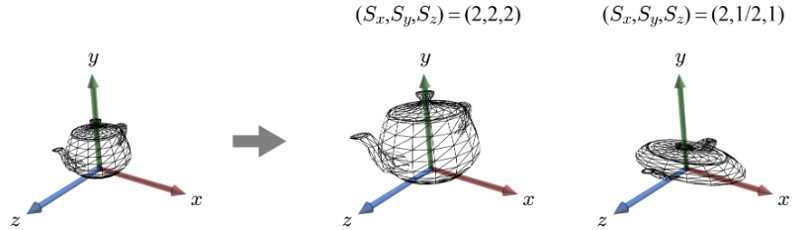
2. 3D Scaling
스케일링 계수 sx,sy, sz를 사용하여 3D 스케일링을 표현한다.
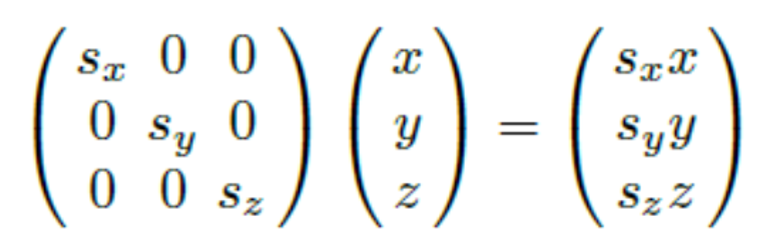
모든 스케일링 계수가 동일하면 스케일링이 uniform하고, 그렇지 않으면 non-uniform 하다고 한다.
3. 3D Rotation
회전 중심이 필요한 2D 회전과 달리 3D 회전은 회전 축이 필요하다.
▪ x축(Rx), y축(Ry), z축(Rz)에 대한 3차원 회전을 생각해 보자
▪ 다음 예는 Rz에 대한 회전을 보여준다. (z축 회전)
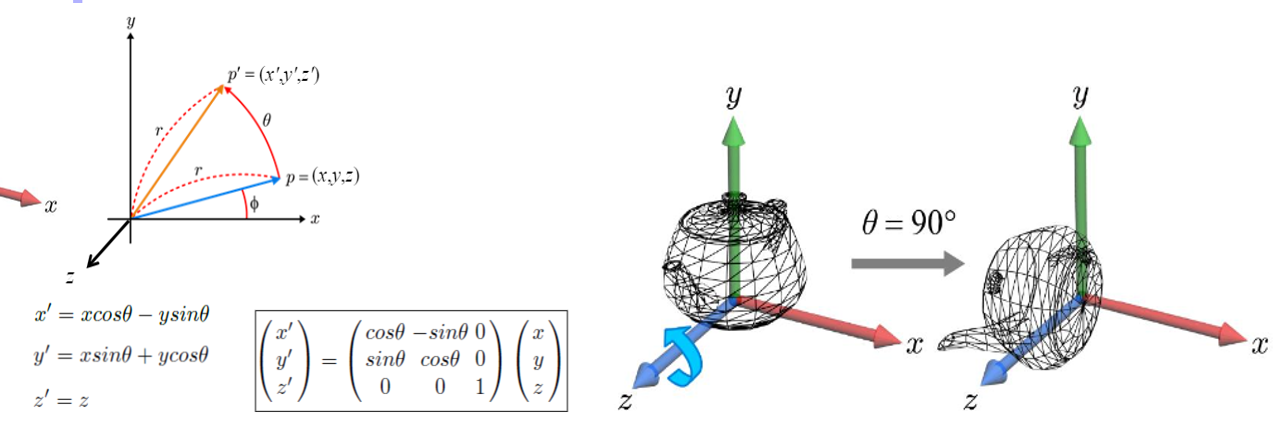
▪ x’ = x.
▪ 오른손의 엄지손가락이 회전축과 일치할 때, 다른 손가락은 y축에서 z축으로 말림을 기억하자.
▪ Rz로 돌아와서 x축에서 y축으로 손가락이 말리는 것을 보면 알 수 있다.
▪ Rz에서 Rx로 이동하면 x축이 y축으로, y축이 z축으로 바뀐다.
▪ 이러한 교체를 확인함으로써 Rx에 대한 행렬을 얻을 수 있다.
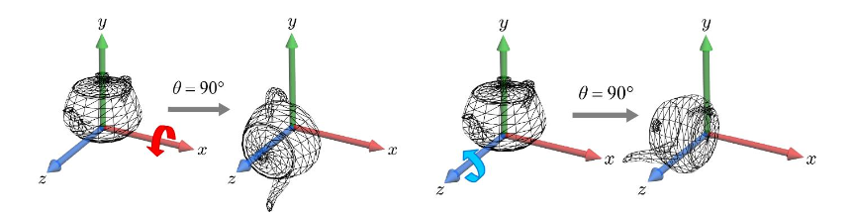
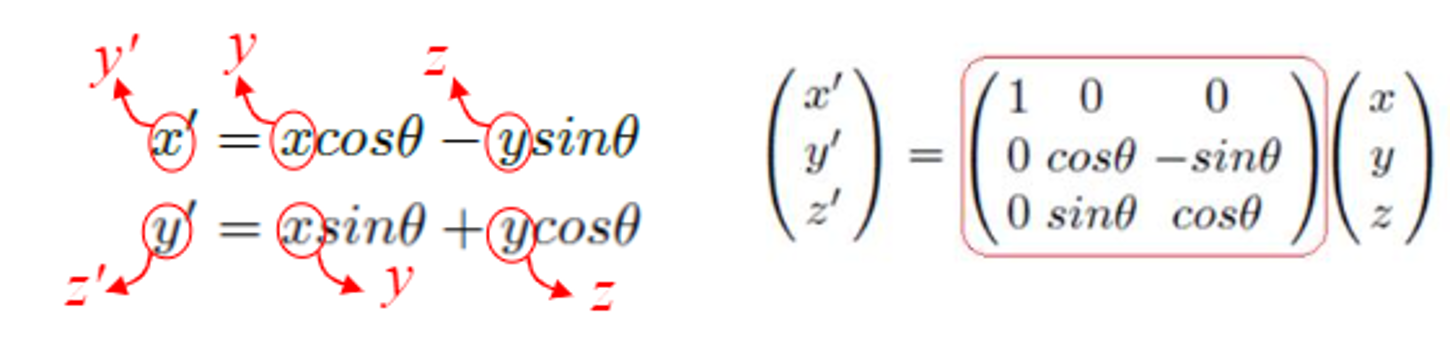
CCW vs CW 회전
▪ 자신을 향하는 축을 기준으로 CCW 회전이면 회전 각도는 양수이다.
▪ 회전이 CW인 경우, 그 행렬은 음의 회전 각도로 정의된다.
▪ -θ만큼 회전하는 것은 2π-θ만큼 회전하는 것과 같다.
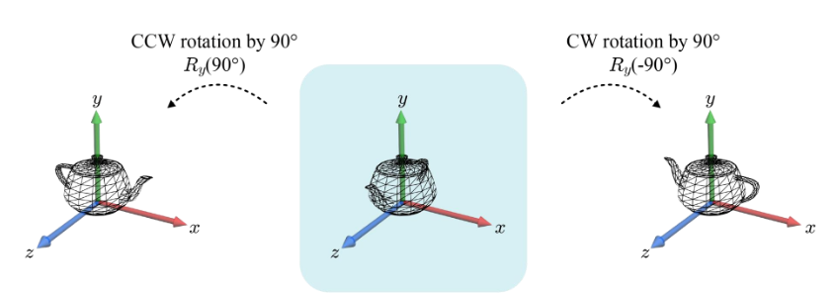
4. World Transform
Object space vs. world space
▪ 객체 생성에 사용되는 좌표계를 object space라고 한다.
▪ 모델의 object space는 일반적으로 다른 모델의 object space과 관계가 없다.
▪ world transform은 모든 모델을 world space라는 단일 좌표계로 조립한다.
+α. Inverse Rotation
회전 행렬 R이 주어지면 열(u, v, n)은 orthonormal basis를 구성한다.
즉, u·u= v·v= n·n= 1 이고 u·v= v·n= n·u= 0 이다.
R의 전치에 R을 곱해 보자.
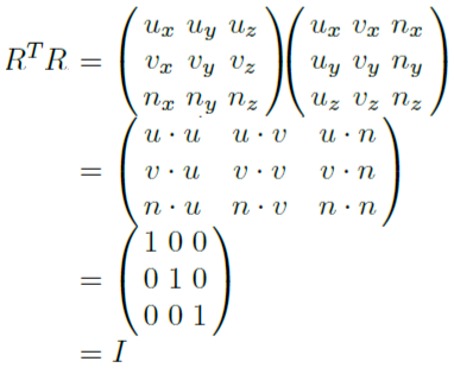
이는 회전 행렬의 역행렬이 전치임을 의미한다.
u, v 및 n이 R의 열을 구성한다는 것을 기억하자. R-1(역)=RT(전치)이므로 u, v 및 n이 R-1(역)의 행을 구성한다.
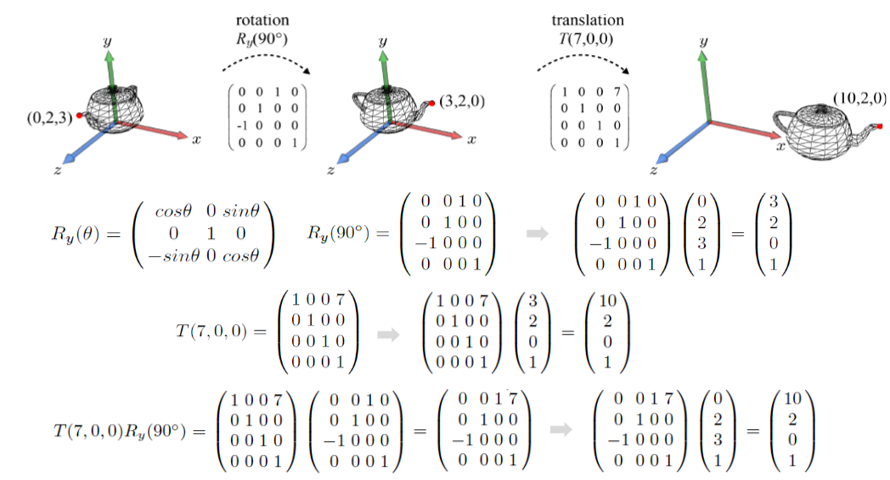
위 개념을 숙지하고, 아래 그림을 이해하자.