그래픽스에서 물체의 회전과 이동을 어떻게 하는지 알아보겠습니다. 따라서 이번 포스트는 그래픽스 개념 보다는 이를 이해하기 위한 사전지식인 선형대수에 더 가깝습니다.
이 포스트는 경희대학교 게임 그래픽 프로그래밍 수업자료를 바탕으로 합니다.
1. 2D rotation
벡터의 2D 회전을 알아보자.
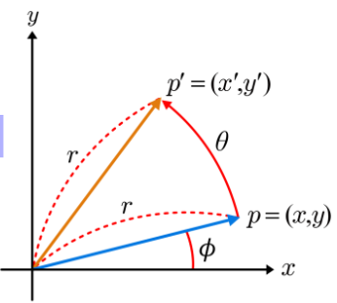
▪ 벡터 p는 원점을 중심으로 θ만큼 회전하여 p ́를 정의한다.
▪ p의 길이가 r일 때 좌표는 (rcosΘ, rsinΘ)이고, 이를 이용하여 p ́의 좌표는 고등학교에서 배운 삼각함수 덧셈 공식으로 다음과 같이 계산할 수 있다.
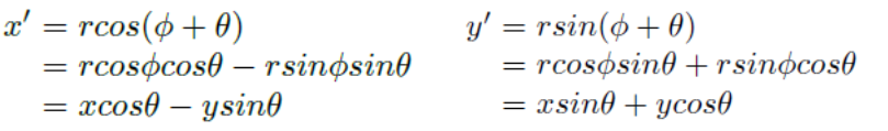
이는 행렬-벡터 곱셈 형식으로 결합될 수 있다.
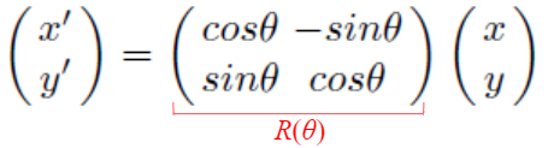
이 공식의 R(Θ)가 rotation matrirx가 된다.
회전의 예시는 다음과 같다.
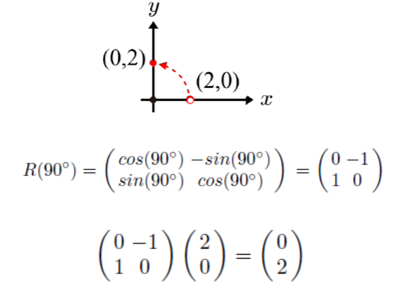
▪ 기본적으로 회전은 시계 반대 방향을 양수로 한다.
▪ 따라서, θ에 의한 시계방향 회전 행렬은 2차원 회전 행렬에 -θ를 대입하여 구한다.
▪ -θ만큼 회전하는 것은 2π-θ만큼 회전하는 같은 것. (R-90°) = R(270°)
2. Translation
▪ Translation은 (x, y)의 점을 (x + dx, y + dy)로 이동하는 것이다.
▪ (dx, dy) translation 벡터를 호출한다.
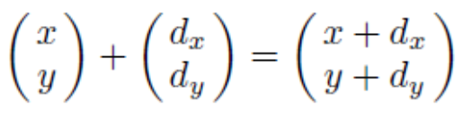
▪ 점의 2차원 데카르트 좌표(x, y)가 주어지면, 3차원 벡터(x, y, 1)를 동차 좌표(homogeneous coordinates)로 사용할 수 있다.
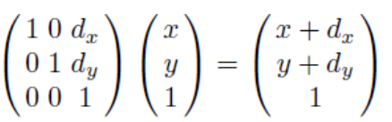
이 식을 위해서는 아래 개념을 이해해야 한다.
homogeneous coordinates
▪ 2D에 점(x, y)이 주어지면 homogeneous coordinates는 (x, y, 1)이 아니라 w가 0이 아닌 (wx, wy, w)이다.
▪ 예를 들어, 데카르트 좌표 (2, 1)을 (2, 1, 1), (4, 2, 2), (6, 3, 3) 등의 동차 좌표로 변환할 수 있다.
▪ 동차 좌표(X, Y, w)가 주어졌다고 가정했을 때, 모든 좌표를 w로 나누면 (X/w, Y/w, 1)을 얻는다. 이는 선의 한 점을 평면에 투영하는 것에 해당한다. w= 1 이고, 처음 두 구성요소(X/w, Y/w)를 데카르트 좌표로 사용한다.
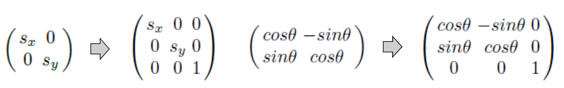
3. 실습
이제 실제로 회전과 이동을 적용시켜 보자. 지금까지 배운 회전과 이동은 원점을 기준으로 설명한 것이다. 먼저 원점을 기준으로 알아보겠다.
▪ 행렬 곱셈은 비가환적이며, 이는 곱셈 순서가 중요함을 의미한다. 아래 예제를 보자.
▪ Rotation (R) followed by translation (T) vs. T followed by R
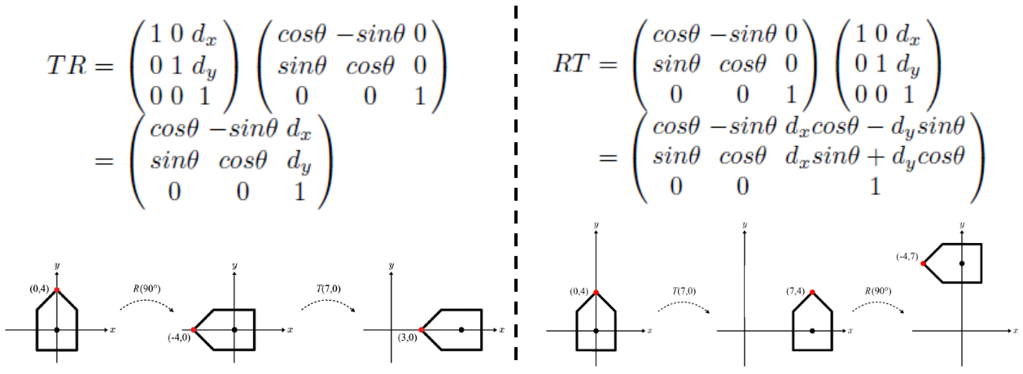
그렇다면, 임의의 점에 대한 회전과 이동은 어떻게 할까?
▪ 임의의 점 (a,b)를 중심으로 (x,y)에서 점 회전은 아래 순서를 따른다.
- (x, y)를 (-a, -b)로 translating
- 원점을 기준으로 translated point 회전
- rotated point를 (a,b)로 back-translating
즉 원점으로 보내고 돌린 후 다시 복귀시키는 것
